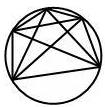
Suppose you take a circle, put some dots along the outside, and then connect them, as in the picture to the left (which has 5 dots on the outside). If only two lines cross at any point, how many regions will the circle be divided into?
Let’s find out! If you place 1 dot along the outside you can’t connect it to anything so you get one region (the entire circle). If you place 2 dots along the outside and connect them you divide the circle into 2 regions. By placing 3 dots along the outside you divide the circle into 4 regions.
Looking at the bottom row, if you place 4 dots on the circle and connect them you get 8 regions. Hey, notice that neat 1, 2, 4, 8 pattern of the title? What about five dots?
At this point it’s getting a little hard to keep track of all the regions, so I colored them in the pictures below.
Looking at the middle of the bottom row, putting 5 dots along the edge divides the circle into 16 pieces, as might be expected.
What if there are 6 dots along the outside? And that’s where everything goes terribly wrong. It only divides the circle into 31 pieces, not 32. Putting 7 dots along the outside is even worse: you get 57 pieces.
It turns out that even though the numbers 1, 2, 4, 8, 16, 31 start off as powers of 2, they’re really following the formula 
So much for our nice pattern.
360 
February 20, 2017 at 12:59 pm |
Also, the divisors of 496 (a perfect number) form the sequence {1, 2, 4, 8, 16, 31, 62, 124, 248}