We sleep HOW MUCH?

I’m an alum of UW-Madison, and have many fond memories of the place (indeed, TwoPi and I met in grad school there).   As a bonus, they have a good alumni magazine.  But even the best magazines make mistakes from time to time, and  the Spring 2009 issue of On Wisconsin includes a graph that is simply wrong.

The graph, illustrating how much time we sleep compared to other activities, appeared in the article “Bedtime Story” (description “Why do we snooze?  UW researchers are pursuing an unconventional theory — that our brains downsize while we sleep, getting us ready to face another day.”)  Here’s what the graph looks like:

Take a look at the two biggest circles:  we spend 36% of our life sleeping, and 19% on other [unlisted] activities.  But that gray circle is pretty small — you could fit 3 or 4 of them into the Sleeping circle.  I grabbed a ruler and, sure enough, its the diameters, not the areas, that have the 36:19 ratio.  The distinction is even more striking when you look at the tiny circles:  we spend 36 times as much of our time sleeping as we do on telephone calls, mail, and email and that’s a LOT, but it’s not a ratio of 1296 (as the areas would suggest).

So I created a graph in which the areas are in correct proportion:

There’s still a clear difference in how much time we spend doing different things, but it no longer looks like 61% of our lives are spent in bed.

Tidal force, or The Moon and the Mosquito revisited

As Ξ noted in an earlier post, the claim that the gravitational pull of a mosquito is stronger than the gravitational pull of the moon is off by a fair bit … roughly five orders of magnitude.

The original author of the claim, George Abell, was an astronomer.  Aren’t astronomers supposed to be good at working with large numbers?  Wondering if he had been misquoted in Scientific American, I set out to find out what I could about this claim.

A google search turned up a fair number of sources that describe Abell’s claims; most of their accounts are similar to that of Lilienfeld and Arkowitz.  One of the more widely read accounts appears in The Skeptics Dictionary (by Robert T. Carroll):

Astronomer George O. Abell claims that a mosquito would exert more gravitational pull on your arm than the moon would (Abell 1979).

The secondary literature is pretty much in agreement: Abell claimed that the mosquito exerts a stronger gravitational pull than the moon.  (And clearly that claim is false.)

A quick stop at the library of a nearby college turned up Abell’s original article.  He had written a piece for the Skeptical Inquirer, a review of a book on the putative effects of the moon on human behavior.  The book’s author had suggested a plausible mechanism for such influence:  the body is largely made up of water, and we all know the moon is a primary cause of tides on the Earth.

Abell’s discussion notes the source of the Moon’s influence on terrestrial tides:  not the gravitational pull of the moon, but rather the difference in that force between the nearest and farthest points on the Earth.  Because of that difference, the Earth is (very slightly) distorted, with its fluid surface in motion attempting to achieve equilibrium.

Abell notes that while the Sun’s gravitational pull on the Earth is more than 100 times stronger than the Moon’s, its tidal force — the difference in the Sun’s pull over the diameter of the Earth — is less than half that of the tidal force of the Moon.

If the Moon’s influence on human behavior were tidal (acting on the fluids in the body), then that tidal effect would  be due to differences in the Moon’s gravitational pull on the fluid in different parts of your body — differences due to the fact that (for a 6 foot tall person) part of their body could be six feet closer to the center of mass of the Moon than other parts of their body.   Abell quotes this difference as being “about one part in 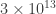(or 30 trillion) of the weight of that fluid”, and states that the copy of a magazine in the reader’s hand is tens of thousands of times more significant in producing tidal forces.

If we take the weight of the magazine to be roughly 1/2 lb [based on weighing a stack of AMS Notices], or 2.2 Newtons, leading to a mass of 0.2 kg, then the tidal force due to the magazine (over distances ranging from .2 m to .5 m — assuming I hold the book about 20 cm from my torso, and my torso is roughly 30 cm deep) will be

(where G is the gravitational constant, and M is the mass of the fluids in your body), which works out to approximately 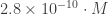newtons.  A similar calculation for the lunar tidal force acting on my body when I am standing (taking my height to be 2 meters):

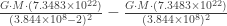
which is roughly newtons.

So indeed, as Abell claimed, it is reasonable to conclude that a small book or magazine in your hand exerts a tidal force on the order of thousands of times stronger than the moon on your body.

But wait!  Where are the mosquitoes?

Abell described a second potential source of lunar influence on the human body.  He writes:

What might matter is the difference between your weight in the presence of the moon’s gravitational effect and what it would be if there were no moon.  At the most, that difference amounts to only 0.01 gram, or about 0.0003 ounces, less than the effect of a mosquito on your shoulder.

In the paragraph leading up to that passage, Abell noted that this isn’t the same as the gravitational pull of the Moon on your body, since the Moon is also pulling on the Earth (so you have a slightly larger acceleration toward the Moon than the center of the Earth does — in effect, this is the tidal force calculation in a different guise).

It isn’t quite clear what Abell means by “the effect of a mosquito on your shoulder”:  is he referring to a gravitational (tidal) effect due to the mosquito, or is he just referring to the weight of the mosquito — the amount by which it increases your weight when it lands?

I’ll leave the analysis of these two interpretations as exercises for our readers.  But the conclusions I found:  if we compute the tidal force of the mosquito on your body, it is far greater than the tidal force of the moon on your body (because of its proximity versus the great distance to the Moon).  If instead we believe that Abell is claiming that the weight (mass) of the mosquito is greater than the 0.01 g that he had computed, then he is wrong:   Ξ had generously estimated the mass of a mosquito at 5 mg; Abell’s estimate of the Moon’s influence on a person’s weight is about twice that.

Abell’s review of Arnold Leiber’s The Lunar Effect: Biological Tides and Human Emotions (1st ed, 1978) appeared in the Skeptical Inquirer 3 (1979) pp 68 – 73.

The Abel Prize in rhyme

There once was a math guy from Russia
Which is just to the east of East Prussia.
He proved many a theorem.
Geometers revere him.
The Abel Committee did gusha.

They said to Mikhail Gromov,
(Whose sweater in this picture looks mauve)
“You are so creative!
A mathematical native!
You’re analysis’s own Brett Favre!”*

His work (expanding thresholds
Of n-dimensional manifolds
And related measure)
Gave people such pleasure
That this year’s Abel Prize he holds.

* No doubt they were referring to Brett’s heyday in the 90s, and not to last season.

For a more interesting but less poetic summary of his life and work, check out the official summary.

The Creative Commons picture of Mikhail Gromov was taken in 2007 by Gert-Martin Greuel.

Inversions

Dave Richeson over at Division by Zero has a post today about ambigrams.  Ambigrams, also known as inversions, are words that have some sort of symmetry.  In the post he shares some of the ambigrams he’s created.

I am, sadly, not so creative.   Fortunately, there are some computer programs that do the work for me!  FlipScript (again from Dave’s article) does a nice job, but they’re strict about copyright (you have to buy the images to be able to show them; still, many are worth buying for a special occasion).

Ambigram.Matic has a more public generator.  The script isn’t as fancy, but they write that the intent isn’t to be a finished product but just a starting place.  Here’s one they came up with:

Not too shabby!  Be sure to take Dave’s warning seriously about these sites, though — they can be amazing time sinks.

Reverse and Add

If you start with a positive integer, reverse the digits, and add that to the original number you sometimes get a palindrome.  For example,  123+321=444, and 1047+7401=8448.

But sometimes you don’t.  In that case, you might need to repeat the process a few times (where “a few” could mean “a lot”).  For example, 498+894=1392, then 1392+2931=4323, and finally 4323+3234=7557.

Based on this, we can define the palindromic order of a number as the number of time that you need to Reverse and Add before coming up with a palindrome.  In the examples above, 123 and 1047 have a palindromic order of 1, while 498 has a palindromic order of 3.  [Presumably under this definition a palindrome like 838 has palindromic order of 0.]  Incidentally, this definition of palindromic order is the one used by Susan Eddings here, as opposed to the one referenced in titles like “Optimization of the palindromic order of the TtgR operator enhances binding cooperativity” in The Journal of Molecular Biology.

So here’s the question:  Does every positive integer have a (finite) palindromic order?  In other words, if you pick a number and repeat this process, possibly neglecting all of your work and home commitments except for feeding the cats and watching The Big Bang Theory, can you be assured that you will eventually get a palindrome?

And the answer is:  I don’t know.  And neither does anyone else, although there’s evidence that the answer is No.

That evidence is the number 196.  If you start with 196, you won’t get a palindrome at first, within 200 steps (as Jason Doucette shows), or even within 700 million iterations.   There are other numbers that appear to have this same awkward non-palindromic property  [for example, 691, and also 295, 394, and a bunch more], but the number 196 is the smallest; in its honor, this “Reverse and Add” algorithm has come to be known as the 196-algorithm.

So spending all your time concentrating on a brute force method of finding out if 196 continues to produce non-palindromes is going to be tedious.  In good news, you could explore other interesting questions:  what do you notice about numbers with palindromic order 1?  Can you find one with palindromic order 4? Which number(s) under 100 has the largest palindromic order?

As a side note, I ran across this property while looking for  interesting mathematical processes that resulted in the sequence 2, 4, 6, 8, 10, 11, [part of my ongoing quest to find Patterns that Fail].  It turns out that if you look at which numbers can be written as the sum of a positive integer plus its reverse, you initially get the sequence 0, 2, 4, 6, 8, 10,  [0=0+0, 2=1+1, up to 10=5+5] but then 11 shows up, since 11=10+01.

The picture above is the Shoulder Sleeve Insignia of the 196th Infantry Bridage.  Isn’t the symmetry a nice parallel to the whole Reverse and Add idea? 196InfBdeSSI.gif

FutureGen

It’s hard to estimate how much it will cost to start/change a company, especially because it’s reasonable to expect that $1 today is worth less than $1 in the future.  Do you use today’s prices, or take inflation into account?  On the other hand, if what you’re doing is comparing costs, it doesn’t really matter which method you use as long as you’re consistent.

A mistake with that last bit ended up possibly costing FutureGen its future.

Here’s some background.  According to the US Department of Energy, “FutureGen is an initiative to equip multiple new clean coal power plants with advanced carbon capture and storage (CCS) technology.”  This was announced in 2003, but a year ago the top folk in the Department of Energy decided that it was going to be too expensive to build.

Certainly it would have been expensive:  over a billion dollars (about 8% of which would have been paid for by China and India as research into cleaner energy that they might be able to use).  But not quite as expensive as they thought.  According to Scientific American,

the Department of Energy (DOE) had essentially forgotten to account for inflation when estimating FutureGen’s projected costs. Specifically, the department had said in 2004 that it would cost $950 million to build, a sum that it last year said had ballooned to $1.8 billion when projected through 2017. In fact, the GAO says, the actual cost considering inflation would be closer to $1.3 billion….

These new figures were released in a 54-page report by the Government Accountability Office (GAO) on March 11, 2009, which you can read here.  In particular, one of the problems was that the Department of Energy was making comparisons of FutureGen as originally planned versus replacing/restructuring, but in one case they were taking inflation into account (that $1 spent in 5 years is worth less than $1 today) and in another case they weren’t, so the numbers weren’t comparable.  In The New York Times, Representative Bart Gordon (a Democrat from Illinois) said,

I am astonished to learn that the top leadership of the Department of Energy in the last administration made critical decisions about our nation’s energy future and capacity to combat global warming based on fundamental budget math errors…This is math illiteracy on a grand scale and with global consequences.

(In the interests of full disclosure, Illinois is the state where FutureGen would be located, so the consequences may have hit closer to home, so to speak.)

With this disclosure and a new administration, FutureGen might be back on the table.  Or maybe not — presumably the price has increased even since those figures were taken into account, and so other comparisons would have to be made before a decison would be made.  Hopefully this time using comparable data.

In Good Company

We were thrilled to learn that we were mentioned in an article about math blogs that Jenni and Jon Ingram wrote for the March 2009 issue of Mathematics Teaching, a journal of The Association of Teachers of Mathematics in the UK.  Most of the articles (like the evocatively named “It would be 19 if 10 was an odd number” or “Puppets Count”) are only available to members, but a few, including theirs, are open to all.

They also wrote about dy/dan, Let’s Play Math!, and MathNotations,  with descriptions both of the blogs and of some samples posts for each.

Thanks for putting us in such good company!

The Beach Photo was taken by Richard Marris during the Kioloa Flickrmeet, Kiola, New South Wales, Australia [creative commons license].

The moon versus the mosquito

Last month Scientific American reported on whether scientific studies showed an association between the full moon and strange behavior.  The short answer is no, despite a wide-spread belief in the connection.

In the article, Scott O. Lilienfeld and Hal Arkowitz  mention that some people (ancient and current) believe that the moon’s supposed effect might have something to do with its gravitational effect on water, which makes up most of the human body.  But then they add that this effect isn’t strong enough:

As the late astronomer George Abell of the University of California, Los Angeles, noted, a mosquito sitting on our arm exerts a more powerful gravitational pull on us than the moon does.

“Hmmm,” I thought to myself upon reading this, “Is that true?  Is a mosquito really a more significant graviational force than the moon?”

The force of gravity between two objects of mass and respectively is given by

where is the gravitational constant and is the radius between the two objects.

In order to compare the force exerted by the moon and a mosquito, and (the mass of the individual) are the same in both equations, so we really just need to compare the values of and .

So what are these two amounts?  NASA says that the mass of the moon is 7.3483×10²² kg, which translates to 7.3483×10²⁸ milligrams. The average distance to the earth is 3.844 x 10⁵ km, which is the same as 3.844 x 10¹¹ mm. [I’m using tiny units because we’re about to compare this to a mosquito.] So the ratio is just about 497,300 mg/mm².  This amount might be an underestimate, too, because the distance I used was the distance between the moon and earth, but I suspect that is the distance between the centers; we only need to go from the center of mass of the moon to the surface of the earth where our individual is sitting.    But for rough purposes, it will do.

Mosquitoes, on the other hand, appear to weigh 1-5 milligrams each (though some sites say only 1-2 milligrams).  We’ll use the upper bound of 5 milligrams.  For the distance, I feel like we should use the distance between the centers of the mass of the mosquito and individual if we want the overall gravitational effect, but I’m willing to limit the effect  to just a few cells near the mosquito.   A reasonable estimate for the distance from the mosquito’s body to the skin is 1 mm.  The formula then becomes only 5 mg/mm².  And this amount is really an overestimate, since I used the largest possible value for the mass and chose the smallest distance.

So if my estimates here are accurate and I haven’t missed anything significant, the gravitational pull of the moon is on the order of 100,000 times as strong as the gravitational pull of a mosquito;  George Abell — debunker of pseudoscience himself — appears to be quite wrong.

Isn’t that a great photo of the full moon?  Luc Viatour took it in Belgium (© Luc Viatour GFDL/CC). The mosquito comes from the Centers for Disease Control and Protection.

Martha Math

I just learned about the show Whatever, Martha! from a friend of mine.  The show consists of Alexis Stewart (Martha Stewart’s daughter) and Jennifer Koppelman Hutt watching and commenting on old episodes of Martha Stewart Living.  Like a domestic version of Mystery Science Theater 3000.

I prefer the one about making s’mores (mostly because, Seriously?  Homemade sticks?) but in an effort to keep it math related I’ll post a 5-minute snippet that has some math.  Here’s the word problem:  if the diagonal of the square is 10½″, what is the side of the square?

(Apparently Martha and her mom have a better relationship than this video would imply.  If Martha Stewart is OK with this, my respect for her has just gone way up.)

Math Teachers at Play #3 is here!

No, not HERE.  It’s ventured away from Let’s Play Math for the first time, and is being hosted over at f(t), a blog by 4^th year math teacher Kate (HEY, she’s just down the road in Syracuse!  Hi neighbor!).  Like the two before it, this edition of Math Teachers at Play has a ton of good stuff in it.  Like this post by Larry Ferlazzo about places to find Math in the Movies (Mathematics in Movies and Math and the Movies!).

(Speaking of Carnivals, does anyone know anything about the current status of the Carnival of Mathematics?  It seems to have stalled, but hopefully will pick up again next week.  But the week was not without carnivals:  jd2718 started the Carnival of ∏, which was met with enthusiasm.  Thanks JD!)

Two is Older than One

And so are three and five, but not four.   I’m Spring Cleaning my Inbox, and I ran across this BBC news article from Feb 26 about the Reading Evolutionary Biology Group (consisting of Dr. Mark Pagel and possibly other people) and how they’re analyzing the change of certain words in English and other Indo-European languages.  According to The Telegraph:

Dr Pagel’s work has shown that the pace at which words evolved depends on how they are used. Numerals are the slowest to change, followed by pronouns, probably because they are used extremely often and have a very precise and important meaning. Nouns evolve more slowly than verbs, and verbs evolve more slowly than adjectives. Words that are used less frequently evolve more quickly than those that are common.

The number One is a pretty old word (although apparently it used to be pronounced with a hard o, like only, and only started sounding like “won” about 600 years ago).  Two ,Three, Five, I, and Who are even older, though not much much [and by “old” they’re talking about thousands, if not tens of thousands, of years].  The number word Four, however, evolved much more recently.  I find that last fact rather intriguing, but my searching skills are failing me in learning more about that; perhaps it has something to do with the fact that four doesn’t sound anything like the Latin quattuor or the Greek tessares.

This research also suggests which words will eventually disappear from English.  One leading contender is “dirty”, because there are a lot of unrelated words across the Ind0-European languages that mean the same thing.   Not surprisingly, no numbers were slated for disappearance.

Universal sets and the Russell paradox

I was working with some students on set theory recently, and we were momentarily puzzled by their textbook’s definition of subset:

Let A and B be two sets contained in some universal set U. […] The set A is a subset of a set B if each element of A is an element of B….  More formally, A is a subset of B provided that for all x ε U, if x ε A then x ε B.

What threw us was the reference to a universal set U.  Why bother with that?  Why wouldn’t we just quantify over all x in A, instead of all x in U?

After a bit of thought, I realized there were a few reasons:

1. This makes defining set equality a bit cleaner:  A=B provided for each x in U, x ε A iff x ε B.  (If we didn’t have a universal set U to refer to, we’d presumably have to do two separate if-then statements, one quantifying over A, the other over B.)
2. It places the formal discussion of set theory in the familiar setting of Venn diagrams.
3. It sets the stage for dealing with set operations (union, intersection, and especially complements).

There is a 4th reason:  a desire to avoid impredicative definitions (according to the Oxford Dictionary of Philosophy, “Term coined by Poincaré ; for a kind of definition in which a member of a set is defined in a way that presupposes the set taken as a whole”;  more loosely, definitions that can potentially be self-referential).

Sidestepping the technicalities,   I wondered if we could easily craft a compelling reason to work within a universal set: what are the consequences of ignoring it?  The obvious place to worry is in computing set complements.  And thinking about self-reference, I wondered what could go wrong in building Ø^c without reference to a universal set?

If we call that complement M (for “monster”, or “massively huge”, or…), we see a set that contains everything that isn’t in the empty set.   “Cool!”, you’re thinking — that’s a great choice for a universal set U!

Well, hold on a bit.  This M has lots of stuff in it.  17, and {17}, and cool mathy stuff like that.  But it also has my old 82 Impala, and every sock I’ve ever lost, and every subset of the set of all socks that I’ve lost.   Everything you can imagine is an element of M.

For that matter, M even contains itself as an element, since M contains every thing as an element.

Once you see that this monster has the bizarre property that MεM, you probably begin to worry.  Maybe we want a smaller universe, that only has the well-behaved stuff, those things in M that aren’t elements of themselves.

Thus we define , the set of reasonable objects.  This set is a better candidate for our universe: it avoids those strange objects that are members of themselves.  (It still has my 82 Impala, though.)

B ut now, is R itself a reasonable object?  Is R ε R ?  If R is a reasonable object, then it should be a member of R, which is a very unreasonable thing for it to do. (That is, if R ε R, then R doesn’t satisfy the membership criteria for R, and shouldn’t be a member of R.)

So apparently then R is unreasonable.  But then we’d expect , which is to say that R is a reasonable object, and thus should be a member of R.

In this way, we’re led to a variation on the Russell Paradox.
Apparently building Ø^c without first pinning down our universe is a bad idea.

The image above is a public-domain harbor map, showing the canning docks in Liverpool England.

Bertrand Russell  first discovered the self-referential paradox of building a set of all sets that are not members of themselves.   He was not (so far as I am aware) related to Baron Russell of Liverpool (Sir Edward Russell), but in any event I shall henceforth look at that image and see “Russell’s Pair of Docks”.

Definitions

What is a planet?

The current definition, from Resolution B5 of the International Astronomical Union, is that

A planet is a celestial body that
(a) is in orbit around the Sun,
(b) has sufficient mass for its self-gravity to overcome rigid body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, and
(c) has cleared the neighbourhood around its orbit.

Pluto hasn’t cleared its orbit, so it’s not a planet.  There’s actually some controversy about this (and as usual, we turn to Wikipedia to learn all about it), but essentially that’s how things stand.  Pluto can at least rest assured that it’s not the first planet to be demoted.

But a lot of people don’t like that Pluto isn’t a planet, and last month the Illinois State Senate adopted a resolution that declared March 13, 2009 as “Pluto Day” and also included the line:

that as Pluto passes overhead through Illinois’ night skies, that it be reestablished with full planetary status

You can read the formal resultion here; it’s a short read, thought it packs no fewer than 10 “Whereas”s into just 1½ pages.   Here’s what is bothering me:  the bill’s sponsor, Senator Gary Dahl, apparently said:

I don’t think we are changing the status of the planet. We’re simply asking that March 13 be declared Pluto Day and that, for the day, Pluto is a planet.

But, if you add Pluto, aren’t you actually changing the definition of Planet?  If not in broad terms, at least by adding “and Pluto”? I get the distinct impression that he doesn’t understand what a definition is.  It reminds me of how our math majors often struggle with definitions when they’re first learning how to write proofs:  starting from the definition of an even integer (twice an integer), it’s initially hard for them to prove that if n is even, then so is n+2.

And yes, I might be making too much of this.  I don’t want to begrudge Pluto its special day.  But still.

Happy Pi Day!

Things that equal Pi

So you want to make a pie for Pi Day, but you don’t want to decorate it with the traditional symbol .  What other expressions could you use that are equivalent?

You could go with the elegant:  a picture of a circle and the ratio of the circumfirence to the diameter

In a similar vein, you could move up a dimension to area

or volume , although in this case you’d have to draw a sphere and I can tell you right now that I’d lose points for clarity.

If geometry isn’t your thing, you could decorate your confection with an infinite sum, perhaps the Madhava-Gregory-Leibniz series (discovered by Madhava of Sangamagram, India about 600 years ago, and then rediscovered by James Gregory of Scotland and Gottfried Wilhelm Leibniz of Germany 200 years later)

or the slightly more complicated

found by Leonard Euler of Switzerland in 1735.  Or even the Bailey-Borwein-Plouffe formula (which is, face it, kind of fun to say) that was discovered only 14 years ago(!) by Simon Plouffe of Quebec, Canada:

Incidentally, Simon Plouffe and Neil Sloane are the authors of the Encyclopedia of Integer Sequences, which gave rise to the online version.

But back to .  Do you prefer products?  Then maybe you’d want to turn to Wallis’s product, discovered by John Wallis of England in 1655:

We’ll end on a more radical note:  the Viète formula, which was named after François Viète of France, but actually found by Euler.